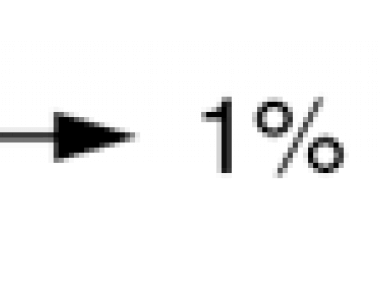3 Frequently Asked Questions About Percentages
What’s the percent increase in a population if it goes from 900 to 981? How can you find 33 1/3% of something? Keep on reading to learn the answers to these and more frequently asked questions about percentages!

While I do read each and every email I receive, the truth is that there simply aren’t enough hours in the day for me to respond to each question individually. But I’ve noticed a lot of commonality to many of your emails, which made me realize that we should dedicate one show each month entirely to your questions…and my answers. Up first today are your most frequently asked questions about percentages.
Sponsor: Squarespace, the all-in-one platform that makes it fast and easy to create your own professional website or online portfolio. For a free trial and 20% off, go to squarespace.com/mathdude and use offer code Mathdude9.
1. How Do You Calculate Percentage Increases?
Math fan Stephanie writes:
“How would I solve the following question: In the year 1986 the population of Elm Town increased from 900 to 981. What was the percent increase? How would I set that problem up to find the answer?”
This type of problem is all about finding what’s called a percentage increase. A percentage increase is simply the amount—expressed as a percentage—that something has increased relative to its original value. If the price of something changes from $100 to $110, the price has increased by $110 – $100 = $10. So to find the percentage change, we just need to compare this $10 change with the original $100 price.
To do that we first need to find the ratio of the amount changed—that’s $10—relative to the original value—that’s $100. In this case that gives us a ratio of $10 / $100 = 0.1. If we then convert this fraction into a percentage (which we can do simply by multiplying the decimal value by 100), we find that the percentage change = 100 * fractional change = 100 * 0.1 = 10%.
Now let’s look at the problem Stephanie brought up about the population of Elm Town increasing from 900 to 981. Since that’s an increase in population of 81 people, the percentage change is 100 * (81 / 900) = 9%. There are many variations on this theme. For example, here’s another question from math fan Teri that at first looks different, but is actually about the same underlying idea. Teri writes:
“If an employee earns $9 per hour and the supervisor wants to give the employee a raise of $3 per hour so in the end the employee will earn $12 per hour, what percentage of the current salary will the increase constitute?”
In this case, the employee’s $9 salary increases by $3 up to $12. The ratio of the amount changed relative to the original value is $3 / $9 = 1/3 or 0.333…. If we convert this decimal into a percentage, we find that the percentage change is equal to 100 * 1/3 = 33 1/3%. A pretty hefty raise!
2. How Do You Calculate 8% of Something?
Math fans Alexis and Max both asked questions along the lines of:
“How do you find 8% of $37.90 in your head? How about something like 33 1/2% of that value?”
As we saw in the episode on using percentages to calculate tips, it’s easy to calculate 1% or 10% of something in your head—but how do you calculate other less simple percentages? To begin with, as we learned before, you can find 10% of any number by simply moving the decimal point one position to the left. So 10% of $5.00 is equal to $0.50. To find 1% of any number, just move the decimal point two positions to the left. So 1% of $5.00 is equal to $0.05.
Once you’ve got those down, it’s easy to find 8% of something since 8% is just equal to 5% + 1% + 1% + 1%. But we don’t know 5%, so how does this help? Well, 5% is just half of 10%, so all we need to do is add half of 10% (or 5%) to 1% + 1% + 1%. Using this type of logic, you can figure out pretty much any whole number percentage you need.
What about something like 33 1/2%? Well, 1/2% is just half of 1%—so you can find 1/2% of any number by first finding 1% of the number and then finding half of this. So 1/2% of $5.00 must be $0.025…or 2.5 cents. In truth, this whole process starts getting kind of cumbersome in situations like this—it’s really intended to be used for making quick mental estimates, not for making precise calculations. At some point, you’re probably better off just using a calculator.
3. Am I Being Short-Changed By Percentages?
Math fan Jane writes:
“I make fudge for a home industry. I sell my fudge for $6.50 per packet. At the shop the lady adds 30% to the $6.50 which gives $8.45 for the selling price. When I collect my money after the fudge is sold out, she just subtracts 30% from the $8.45 which gives me only $5.92. Is that right?”
In short, no. I’d say you’re being short-changed by a sneaky percentage calculation. I’m guessing this mistake is completely unintentional, but nonetheless it is a mistake. The important thing is that you sold her your fudge for $6.50. What she sells it for is irrelevant to you. Which means that whenever she sells a packet of your fudge, you should receive $6.50 and she should keep her $1.95 profit. After all, if you agree to sell it to her for $6.50, she should pay you $6.50!
Wrap Up

In the meantime, be sure to check out my mental math audiobook called The Math Dude’s 5 Tips to Mastering Mental Math. And for even more math goodness, check out my book The Math Dude’s Quick and Dirty Guide to Algebra.
Remember to become a fan of the Math Dude on Facebook where you’ll find lots of great math posted throughout the week. If you’re on Twitter, please follow me there, too. Finally, please send your math questions my way via Facebook, Twitter, or email at mathdude@quickanddirtytips.com.
Until next time, this is Jason Marshall with The Math Dude’s Quick and Dirty Tips to Make Math Easier. Thanks for reading, math fans!
FAQ graphic from Shutterstock.
You May Also Like…