QDT
Latest from quick and dirty tips
A Money Girl listener named Eric says, “I really appreciate listening to your show and all the great information you give. I have a question reg...
In today’s world, marketing for law firms is undergoing significant changes due to new technologies, changing client behaviors, and increased co...
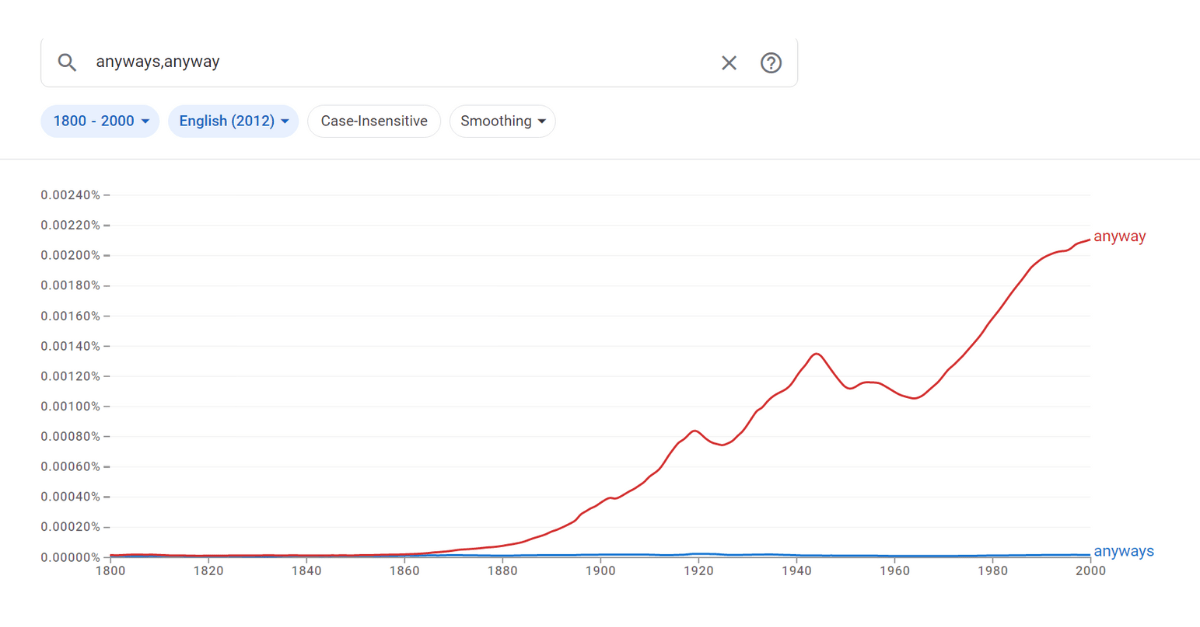
Anabell asked, “Is it correct or incorrect to say ‘anyways’ to someone? As in ‘Anyways, call me later!’ ‘Anyways&r...
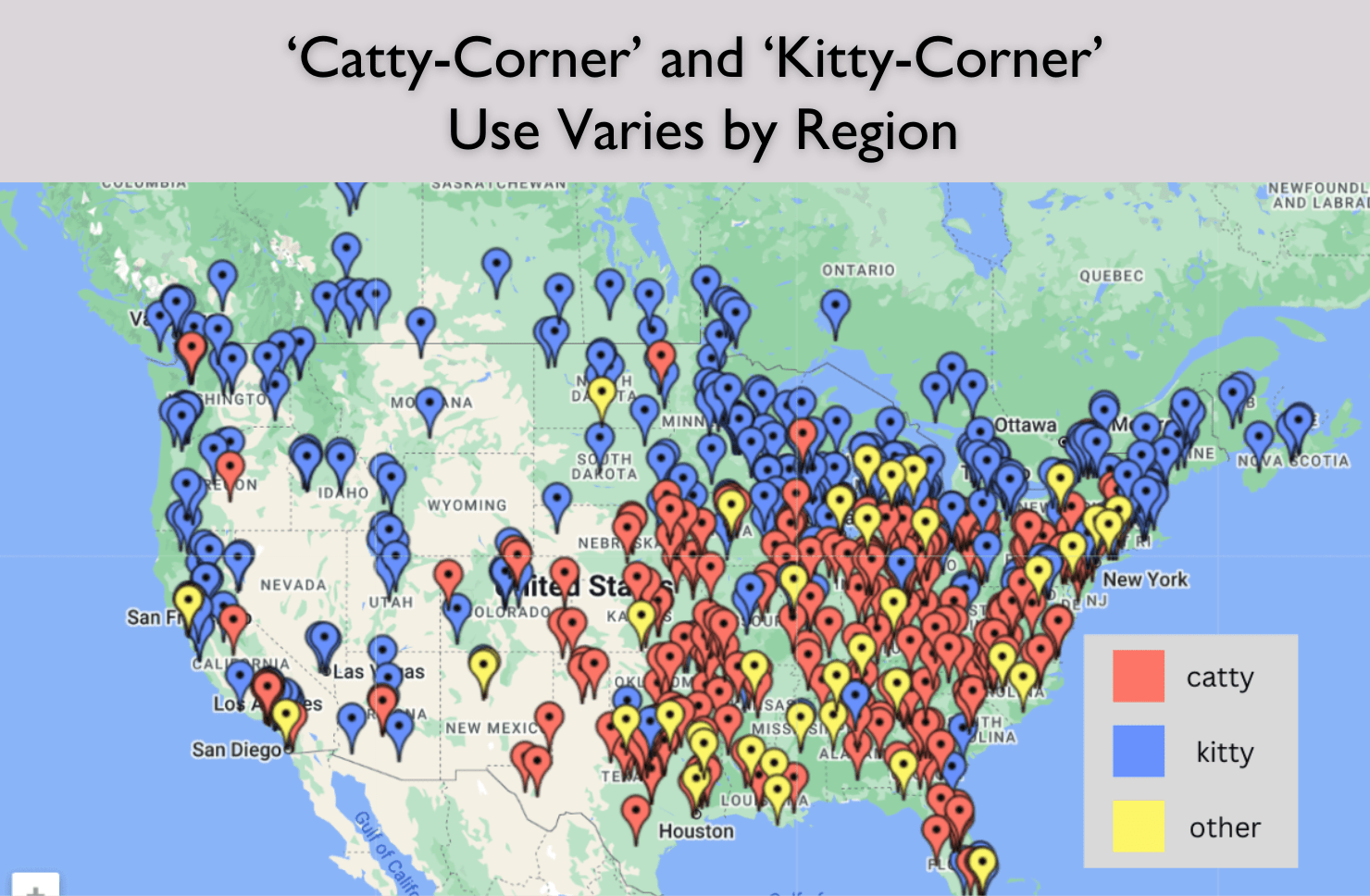
If you watched the recent “Curb your Enthusiasm” finale on HBO, you may have been delighted to see the old Americanism “catawampus&r...
Embarking on a journey to Madrid promises an enchanting experience filled with rich culture, delectable cuisine, and captivating sights. However, to t...
HOST SHOWCASE

Grammar Girl
Mignon Fogarty
Mignon Fogarty is the founder of the Quick and Dirty Tips network and creator of Grammar Girl, which has been named one of Writer's Digest's 101 best websites for writers multiple times. She is also an inductee in the Podcasting Hall of Fame.

Curious State
Doug Fraser
Unexpected gems of knowledge are hidden all around us. Let’s dig them up, one offbeat question at a time.

Get-Fit Guy
Kevin Don
Get-Fit Guy will give you the fitness tools to rise above your former self and achieve the healthy balance between athletic performance and an enjoyable life.

Money Girl
Laura Adams, MBA
From credit, to taxes, to retirement, to insurance – Money Girl makes money simple so you rule your finances, make smart investment decisions, and have a richer life.

Project Parenthood
Nanika Coor, Psy. D.
Parenting is tough. But with Project Parenthood's practical advice, tips, and tricks you’ll add more balance, perspective, and fun into your family’s busy life!

Relationship Doctor
Rachel Vanderbilt, PhD
Dr. Rachel Vanderbilt is a relationship scientist whose research examines how we communicate in our romantic relationships. On the Relationship Doctor podcast, she'll share evidence-backed research on how to live, love, and communicate with your partner.

Modern Mentor
Rachel Cooke
Modern Mentor is your guide to leadership and communication, helping you craft a workplace experience you can feel good about.

Nutrition Diva
Monica Reinagel, MS, LD/N, CNS
Nutrition Diva will help you sort food facts from fiction, separate the good information from the bad, and make eating healthy just a little bit easier – and a lot saner.

Savvy Psychologist
Dr. Monica Johnson
Meet life’s challenges with evidence-based research, a sympathetic ear, and zero judgment. Savvy Psychologist uses the best of psychology to help you be happier, healthier, and most importantly, yourself.

Unknown History
Giles Milton
Unknown History brings you surprising, quirky, and remarkable tales from the past, so you can pretend you paid attention in history class!

Who Knew?
Bruce and Jeanne Lubin
Who Knew collects time-tested household tips and lifehacks to help you live better, solve everyday problems, and save money! Gain the practical wisdom you need to make the most of every day and every dollar!

Modern Manners Guy
Richie Frieman
Live a more polite life in your personal and professional worlds with Modern Manners Guy’s humorous, down-to-earth approach to 21st-century etiquette.
Sign Up for Our Newsletters
Never miss another tip! Join our list to get updates from your favorite hosts delivered straight to your inbox
Sign Up for Our Newsletters
Never miss another tip! Join our list to get updates from your favorite hosts delivered straight to your inbox












.jpg)
.png)