A triangle's angles add up to 180 degrees because one exterior angle is equal to the sum of the other two angles in the triangle. In other words, the other two angles in the triangle (the ones that add up to form the exterior angle) must combine with the third angle to make a 180 angle.
You know how the angles of a triangle always add up to 1800? Why is that? After all, 1800 is the angle that stretches from one side of a straight line to another—so it’s kind of weird that that’s the number of degrees in the angles of a triangle.
What in the world does a triangle have to do with a single straight line? As it turns out, quite a lot. And triangles also have a lot to do with rectangles, pentagons, hexagons, and the whole family of multi-sided shapes known as polygons.
We’ll see exactly what I mean by this over the next few weeks. But for today, we’re going to start by figuring out exactly why it is that the angles of a triangle always add up to 1800. Or so you thought … because we’re also going to see that sometimes they don’t.
First, a review: types of triangles
A quick refresher: there are three different types of basic triangles. They are equilateral, isosceles, and scalene.
- An equilateral triangle has three sides of the same length
- An isosceles triangle has two sides of the same length and one side of a different length
- A scalene triangle has three sides of all different lengths
The length of a triangle’s side directly affects its angles.
RELATED: What is Pascal’s Triangle?
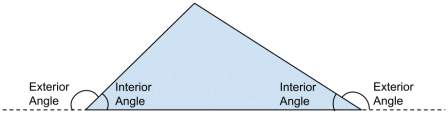
Interior and exterior angles
Before we get too far into our story about triangles and the total number of degrees in their three angles, there’s one little bit of geometric vocabulary that we should talk about. And that is the difference between an interior and an exterior angle.
The easiest way to describe the difference between these two things is with an example. Since today’s theme is the triangle, let’s talk about the interior and exterior angles of a triangle. In short, the interior angles are all the angles within the bounds of the triangle. In other words, they’re the kind of angles we’ve been talking about all along.
The exterior angles of a triangle are all the angles between one side of the triangle and the line you get by extending a neighboring side outside the bounds of the triangle. If you think about it, you’ll see that when you add any of the interior angles of a triangle to its neighboring exterior angle, you always get 1800—a straight line.
Why do triangles have 180 degrees?
Which brings us to the main question for today: Why is it that the interior angles of a triangle always add up to 1800? As it turns out, you can figure this out by thinking about the interior and exterior angles of a triangle. To see what I mean, either grab your imagination or a sheet of paper because it’s time for a little mathematical arts-and-crafts drawing project.
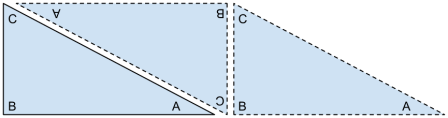
Start by drawing a right triangle with one horizontal leg, one vertical leg, and with the hypotenuse extending from the top left to the bottom right. Now make a copy of this triangle, rotate it around 1800, and nestle it up hypotenuse-to-hypotenuse with the original (just as we did when figuring out how to find the area of a triangle). Finally, make yet another copy of the original triangle and shift it to the right so that it’s sitting right next to the newly-formed rectangle. With me so far? If so, your picture should look like this:
What’s the point of this picture? Take a look at the interior angle at the bottom right of the original triangle (the one labeled “A”). Now take a look at the two angles that make up the exterior angle for that corner of the triangle (the ones labeled “B” and “C”). As we know, if we add up the interior and exterior angles of one corner of a triangle, we always get 1800. And our little drawing shows that the exterior angle in question is equal to the sum of the other two angles in the triangle. In other words, the other two angles in the triangle (the ones that add up to form the exterior angle) must combine with the angle in the bottom right corner to make a 1800 angle.
RELATED: The World of Trigonometry
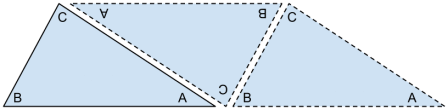
For the sake of simplicity, we’ve made our drawing using a right triangle. But it turns out that you can make an exactly analogous drawing using any triangle you fancy, and you’ll always end up reaching the same conclusion. Try making a few drawings starting with different triangles of your choosing to see this for yourself. As an example, here’s another one that I’ve made:
The inevitable conclusion of this game is that the interior angles of a triangle must always add up to 1800. Our lovely and elegant little drawing proves that this must be so.
Or does it?
Can triangles have more than 180 degrees?
Might there be some limitation to our drawing that is blinding us to some other more exotic possibility? Here’s something for you to think about or try. Procure an uninflated balloon, lay it on a flat surface, and draw as close to as perfect of a triangle on it as you can. If you have a protractor handy, it’d be great to measure and add up the triangle’s interior angles and check that they’re pretty close to 1800.
Now blow up the balloon and take a look at your triangle. What happened to it? If you have that protractor, try once again to sum up its interior angles. What happened to this sum? Do you still get 1800? What does this all mean when it comes to the question of whether or not the interior angles of a triangle always add up to 1800 as we seem to have found?
Thankfully, I have the answer. Head on over to next week’s article where we started exploring the strange and wonderful world known as non-Euclidean geometry.

.png)