What Is the Pythagorean Theorem?

Almost everybody has heard of the Pythagorean Theorem. Heck, even the brainless Scarecrow from the Wizard of Oz knew about it. Remember? When he receives his diploma from the “Wizard” at the end, he declares: “The sum of the square roots of any two sides of an isosceles triangle is equal to the square root of the remaining side.”

Those of you who are already familiar with this famous theorem may have noticed a little problem here since the Scarecrow—or maybe the screenwriters—got it wrong! Perhaps it was just that he didn’t receive a brain after all? What should the Scarecrow have said? By which I mean what does the Pythagorean theorem really say? That’s exactly the question we’ll be answering today.

Sponsor: Netflix Instant Streaming. Watch thousands of TV episodes and movies on your PC, Mac, iPad, iPhone or TV instantly. All streamed instantly to you by Netflix, saving you time, money, and hassle. For your free 30-day trial, go to Netflix qdt.

The Pythagorean Theorem

In words, the Pythagorean Theorem says that the lengths of the two legs of a right triangle—which is a triangle in which two sides come together to form a right angle—have a very special relationship to the length of its long side…aka, its hypotenuse. Specifically, if you square the lengths of the two legs and add the resulting numbers together, that number will always equal the square of the length of the hypotenuse.

Words are nice, but we’ve been talking about algebra lately, so let’s see what the Pythagorean Theorem looks like in terms of variables a, b, and c. Namely:

a^2 + b^2 = c^2

What do the symbols a, b, and c here mean? Well, a and b represent the lengths of the shorter legs of the triangle, and c represents the length of the hypotenuse. If you think about it for a minute, you’ll see that this formula “says” the exact same thing as the more wordy description from before…but it’s a lot more concise.

How to Use the Pythagorean Theorem

The beauty of this algebraic form of the Pythagorean Theorem is that I can tell you the lengths of the legs of any right triangle, a and b, and you can tell me how long the hypotenuse, c, has to be. Just to make sure this is true, let’s check and see if it works for the ingenious rope that Knot Dude—the hero of last week’s episode—used to help his father build the Great Pyramid of Giza.

As you’ll recall, Knot Dude’s rope triangle had a=3 and b=4. Since a^2=9, b^2=16, and a^2 + b^2 is therefore equal to 9 + 16 = 25, the Pythagorean Theorem tells us that c^2—the square of the length of Knot Dude’s triangle’s hypotenuse—must also equal 25． Is that true? Well, the length of the hypotenuse of Knot Dude’s triangle was 5, which means that c^2 was indeed equal to 25． The Pythagorean Theorem works!

Who Was Pythagoras?

As a quick aside, have you ever wondered where the word “Pythagorean” comes from? The short answer is that Pythagoras was a Greek dude who lived a really, really long time ago…about 2,500 years! Given this length of time, it shouldn’t be too surprising that many of the details of Pythagoras’ life are a little fuzzy.

But we do know that he was a philosopher and a mathematician, and that he started a kind of religious movement known as “Pythagoreanism” where, among other things, everybody was a vegetarian and lived in awe of the awesomeness of math. Although others had certainly discovered the relationship between the lengths of the sides of right triangles that we’ve talked about, Pythagoras wrote about it and, well, the rest is history…literally.

Pythagorean Triangles

Getting back to triangles, it’s clear that Knot Dude’s 3–4–5 triangle (those are the lengths of the three sides) is special. But how special is it? Are there other triplets of whole numbers that satisfy a^2 + b^2 = c^2? For example, does a triangle with, say, a=2 and b=4 work? If you try it out, you’ll see that this doesn’t work because the resulting value of c we get from the Pythagorean Theorem is not a whole number.

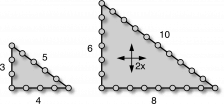
So maybe there aren’t any other right triangles with whole number sides. Actually, there are an infinite number of them! And I can say this without even having to plug in a single number to check. How can I be so sure? Take a look at this:

The only difference between the left and right triangles here is that I’ve scaled the one on the right up to be twice as big as the one on the left. In other words, the legs that were 3 and 4 units long on the left are doubled to be 6 and 8 units long on the right. Which means that all the sides of the bigger triangle are still whole numbers. And, therefore, it means that Knot Dude’s 3–4–5 triangle is not the only right triangle with whole number sides.

If you think about it, you’ll see that instead of doubling the sides of the triangle, we could have multiplied them all by 3, 4, or any other whole number. And, as you can verify, each of these scaled-up triangles satisfy the Pythagorean Theorem, too. Which means that they’re all right triangles with integer length sides and are therefore known as “Pythagorean triangles.”

What Are Pythagorean Triples?

The lengths of the sides of Pythagorean triangles are known as “Pythagorean triples.” So (3, 4, 5) is a Pythagorean triple, as is (6, 8, 10), (9, 12, 15), and so on. Are there other Pythagorean triples besides these simple scaled-up ones that we’ve obtained by multiplying the lengths of Knot Dude’s 3-4-5 triangle by various integers?

Maybe, maybe not—I’m not going to tell you right now. Instead, I’m going to let you think about it for a bit and see if you can come up with any others. Be sure to check back next week for the answer and explanation.

Wrap Up

Okay, that’s all the math we have time for today. If you want to learn more about algebra, please check out my book The Math Dude’s Quick and Dirty Guide to Algebra.

Remember to become a fan of the Math Dude on Facebook where you’ll find lots of great math posted throughout the week. If you’re on Twitter, please follow me there, too. Finally, please send your math questions my way via Facebook, Twitter, or email at mathdude@quickanddirtytips.com.

Until next time, this is Jason Marshall with The Math Dude’s Quick and Dirty Tips to Make Math Easier. Thanks for reading, math fans!