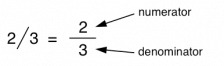
The fraction 1/2 means “one piece of a whole object divided into two equally sized parts.” The denominator indicates that two parts make a whole, and the numerator counts off the fact that the fraction 1/2 contains one of those parts. The fraction X/Y means “X pieces of a whole object that is divided into Y equally sized parts.”
In the last article, we discovered that integers alone are not sufficient to fully describe the world around us—we need the fractions existing between the integers too. (In learning that, we also learned that fractions are not integers.) In fact, eventually, we’re going to discover that even fractions won’t fully satisfy our needs! But we’ll leave that for a future article—there’s still much to learn about the fractional world first.
In particular, today we’re going to take a deeper look at fractions and learn a few quick tips to help you understand exactly what numerators and denominators tell you.
What are fractions?
Before we get too far into the details of what the various parts of a fraction mean, let’s briefly review their anatomy. First, a fraction is made up of two integers—one on the top, and one on the bottom.
The top one is called the numerator, the bottom one is called the denominator, and these two numbers are separated by a line. The line can be horizontal or slanted—they both mean the same thing and simply serve to separate the numerator from the denominator.
How to pronounce fractions in English
If you’ve known about fractions for a while, it’s probably been some time since you’ve contemplated the names we use to describe them. But they aren’t exactly obvious, so it’s worth spending a minute or two thinking about them.
Here’s the quick and dirty tip to help you remember how to pronounce them all: The numerator is always spoken first, and you pronounce it exactly as you pronounce the number. For example, in 1/2 the numerator, 1, is just pronounced “one;” or in 45/77 the numerator, 45, is simply pronounced “forty-five.” Easy enough. But denominators are a bit trickier. They use the following convention:
- 2 is pronounced “half”
- 3 is pronounced “third”
- 4 is pronounced “fourth” (or “quarter”)
- 5 is pronounced “fifth”
- 6 is pronounced “sixth”
- 7 is pronounced “seventh”
- 8 is pronounced “eighth”
- 9 is pronounced “ninth”
- 10 is pronounced “tenth,” and so on.
So, for the fraction written 1/2, the denominator, 2, is pronounced “half,” and the entire fraction is therefore “one-half.” A little less obvious: For the fraction 45/77, the denominator, 77, is pronounced “seventy-seventh,” so the entire fraction is “forty-five seventy-sevenths.”
An easy way to remember this is that with the exceptions of “half” and “quarter,” the words used to describe the denominator of a fraction are the same used to put things in order—for example, the order in which runners finish a race: “third,” “fourth,” “fifth,” etc.
What is a denominator?
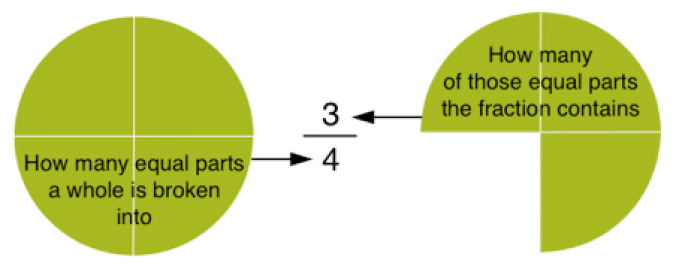
Now let’s take a closer look at the different parts of a fraction. First, the bottom part—the denominator. The word “denominator” is derived from the Latin word “nomen,” which means “name” (and also shows up in words like “nominate” and “nomenclature”). And that’s pretty much what the denominator of a fraction does: it “names,” or indicates, the type of fraction that is described by the numerator (the top part).
What does the denominator tell you?
Here’s what I mean. The denominator of a fraction tells you how many parts a whole is broken into. It can be a whole pineapple, a whole song, or a whole anything. If the denominator of a fraction is, say, 4, then that indicates that the whole whatever is broken up into 4 equally-sized pieces.
Or, if the denominator is 12, that means the whole whatever is broken-up into 12 equally-sized pieces. But how exactly does that “name” the type of fraction? Well, that leads us to the meaning of the numerator.
What is a numerator and what does it tell you?
The word numerator comes from the Latin verb “enumerate,” which we still use in English to mean “to count.” So, the numerator of a fraction counts the number of equally-sized pieces (identified by the denominator) that are contained in the fraction.
How, then, do we put this all together to understand the meaning of fractions? Here’s the quick and dirty tip: Going back to our examples from before, the fraction 1/2 means “one piece of a whole object divided into two equally sized parts.” The denominator indicates that two parts make a whole, and the numerator counts off the fact that the fraction 1/2 contains one of those parts. Similarly, the fraction 45/77 means “forty-five pieces of a whole object that is divided into seventy-seven equally sized parts.”
What does it mean if the numerator is bigger than the denominator?
In all the examples so far, the numerator has always been smaller than the denominator. In other words, in 1/2 and 45/77, 1 and 45 are smaller than 2 and 77, respectively. But what would it mean if the numerator were bigger than the denominator? Something like 7/4?
Well, let’s try interpreting this the same way as before. The denominator, 4, indicates that a whole is divided into four equally sized parts, and the numerator, 7, indicates that we have seven of those parts. So, if four parts make a whole, and we have seven, then we must have a whole object plus three more of the equally sized parts. So 7/4 is equivalent to 1 3/4—also known as “one and three-quarters”—and we now know that a fraction whose numerator is greater than its denominator represents a number that is greater than one. In case you’re wondering, that type of fraction is called “improper,” whereas fractions like 1/2 with numerators less-than denominators are called “proper.”
What does it mean if the denominator is less than one?
So far we’ve only talked about fractions with denominators that are greater than one. At the end of the last article, I asked the “brain-teaser” question: “Why can’t the denominator of a fraction be zero?” To find out the answer to that question, and take a peek at how fractions with denominators less-than one work, check out last week’s Math Dude Video Extra! episode posted to YouTube and the videos section of the Math Dude’s Facebook page.
Who uses fractions?
In short: Everyone! You’ve probably used fractions without even realizing it.
Let’s say your grandma bakes six cookies. She says that you and your two cousins can each have one, and then asks you to put the rest in a plastic bag. That means 3/6 of the cookies will be eaten and 3/6 will be saved. Once the 3 cookies are put away, you give 1/3 of the batch to one cousin, 1/3 to your other cousin, and keep 1/3 to yourself. You don’t even think of it as using fractions to divide the batch, but that’s what’s happening!
But what about your grandma? She used fractions when she was baking the cookies.
But what about your grandma? She used fractions when she was baking the cookies. The recipe might have called for one cup of flour, a quarter-cup of sugar, and two eggs for a full batch of cookies. She only wanted to make half a batch, so she divided the recipe in half. That means she used 1/2 cup of flour, 1/8 a cup of sugar, and one egg to make the dough for this completely hypothetical (and probably inedible) recipe.
Later, you and your cousins head to the mall to get some new games. You’re in luck—everything in the store is 30% off! That means if you calculate what 3/10 of the original price of the game you want is, you can subtract that number from the original price and figure out what your discounted total would be.
Fractions are so common we treat them like second nature!

.png)