How to Prove the Pythagorean Theorem

It’s summertime here in the northern hemisphere, which means it’s that special time of year when parents of school-aged children are frantically looking for stuff for their kids to do.

If that describes your life right now, I have good news for you. Because today we’re talking about an arts-and-crafts inspired project that you and your kids can do together. It’s sure to keep you busy for at least a little while and it’ll even teach everybody a thing or two about mathematical thinking along the way. And, of course, it’ll be all kinds of good times.

So, without further ado, let’s get started.

What Is the Pythagorean Theorem?

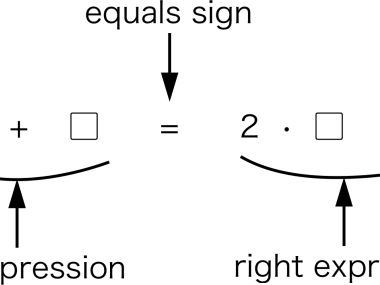
As we’ve talked about previously, the famous Pythagorean Theorem can be expressed in equation form as a² + b² = c²—where a, b, and c are the lengths of the sides of a right triangle. As we’ve also talked about, the point of this (or any other) equation is to say that the combination of variables in the expression on the left side of the equals sign must have the same value as the combination of variables in the expression on the right.

At least that’s the algebraic way of thinking about things. And while this view is all well and good—and indeed a very useful way of viewing the world—it’s also good to keep in mind that it’s not the only possible view. For example, we can also picture the meaning of the Pythagorean Theorem graphically.

How to Think About the Pythagorean Theorem

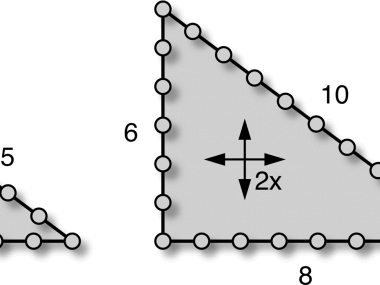
To see how a picture can help us understand the Pythagorean Theorem, let’s draw one. In particular, let’s draw a classic 3–4–5 right triangle with legs that are 3 and 4 units long (so a = 3 and b = 4) and a hypotenuse whose length is given by the square root of a² + b². So c = √25 = 5. I encourage you to engage your crafty side from here on out, to bust out a pencil and paper, and to start sketching things out. Here’s my version of the drawing to get you started.

In this picture, we see the two legs and the hypotenuse of the 3–4–5 right triangle. Notice that each side of the triangle is also one side of a square.
For fun, let’s draw the three squares attached to each side of the triangle. Each of these squares consists of a whole number of 1-by-1 unit area boxes.
When you do that, you’ll find:

• The smallest square has an area of 3 × 3 = 9 boxes (since each side is 3 boxes long).
• The middle square has an area of 4 × 4 = 16 boxes.
• The largest square, next to the hypotenuse, has an area of 5 × 5 = 25 boxes.

Notice that 9 boxes + 16 boxes is equal to 25 boxes. Which means that this picture is showing us that we can think about the Pythagorean Theorem geometrically in terms of combining the areas of boxes.

At this point you should stop and ponder the fact that problems in math can often be looked at in multiple ways. it’s a fact that we don’t often think about, but it’s incredibly important to remember when things starts getting complicated. If you spend a minute thinking about the big picture, you’ll often realize that there’s a simpler way to think about and understand a problem.

Is the Pythagorean Theorem Always True?

While this graphical way of thinking about the Pythagorean Theorem is cool, it really only proves the theorem for the special case of a 3–4–5 triangle. In truth, we could use the exact same method of counting areas to visually show that the Pythagorean Theorem is true for any right triangle with whole number length sides—the family of triangles known as Pythagorean triples—because we once again could simply start adding up areas of squares.

But most right triangles aren’t Pythagorean triples. For example, the triangle built from a pair of 1 unit long legs has a hypotenuse of length √2. And √2 is an irrational number, which means that it’s impossible to divide the √2 length hypotenuse of this 1–1–√2 triangle into an even number of boxes. So it’s also impossible for us to use our visual proof with boxes for this triangle.

Which might make you wonder: Is the Pythagorean Theorem always true? Are there certain right triangles for which it doesn’t work?

How to Prove the Pythagorean Theorem Arts-and-Crafts Style

Not to spoil the big surprise ending for you, but it turns out the Pythagorean Theorem is indeed always true—it works for every single right triangle. To see why, we need to take a slightly different tact and draw a slightly more complicated picture. So that’s what we’re going to do—and when I say “we’re” going to do it, I mean it. Because in order for this to make sense, you’re going to need to take a good look at the picture I’m about to describe. And after staring at it, you’re going to need to redraw it, cut it up with scissors, and play around with the various shapes you create. This is the fun arts-and-crafts part of the project, so don’t skip it!

Just like before, we’re going to start by drawing a right triangle as well as the squares a², b², and c² that extend out from its sides. Next, we’re going to draw two identically-sized squares—one which completely surrounds a² and b², and the other which completely surrounds c². Now, it’ll probably be helpful to redraw each of these two big identically-sized boxes and everything they contain so that you can see the details a bit better—one should enclose the square c², and the other should enclose the squares a² and b².

Now, do you see what’s so awesome here? If not, take a good look at those four curvy lines with arrows. They show that each of the 4 white triangles in the left box fit perfectly into one half of the 2 white rectangles in the right box (if you don’t believe me, redraw the picture, cut up the pieces, and see for yourself). Since the two big exterior boxes are the same size, the fact that all of the white area on the left corresponds to all of the white area on the right means that the leftover area on the left (that is, the square c²) has to be the exact same size as the leftover area on the right (that is, the sum of the two squares: a² + b²).

What does that mean? If you think about it, you’ll see that it means that we’ve just successfully proven that a² + b² = c² for all right triangles. And it means that we have therefore proven that Pythagoras was right!

Wrap Up

Okay, that’s all the math we have time for today.

For more fun with math, please check out my book, The Math Dude’s Quick and Dirty Guide to Algebra. Also, remember to become a fan of The Math Dude on Facebook and to follow me on Twitter.

Until next time, this is Jason Marshall with The Math Dude’s Quick and Dirty Tips to Make Math Easier. Thanks for reading, math fans!

Pythagorean Theorem image from Shutterstock.